The Trammel Method
A trammel is an impediment to freedom or motion. By placing some geometric restrictions on the motion of a pen or pencil, specific types of figures can be drawn. The trammel method is one of many ways to apply this principle to the construction of ellipses (circles and ovals). It’s particularly handy if you need to draw a large curve without a compass.
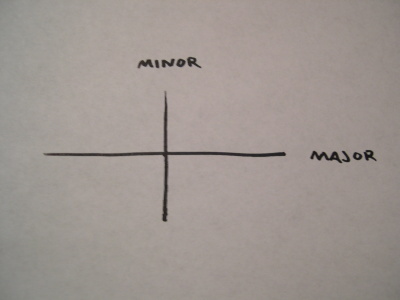
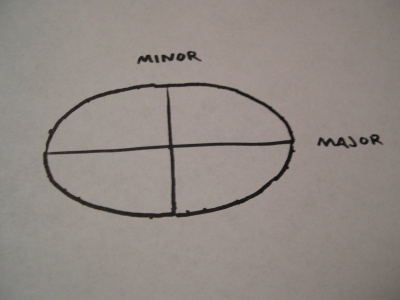
Draw a pair of perpendicular lines where you’d like to place an ellipse. I’ve labeled them as major (long) and minor (short) axes.
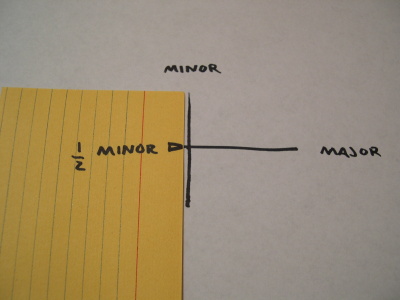
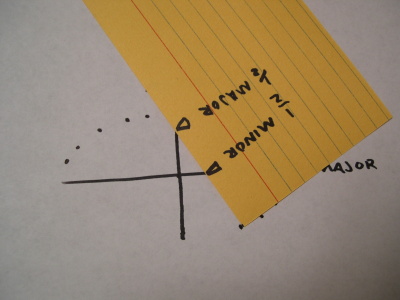
On a piece of scrap paper, mark the length of a minor radius. (Place the corner of the scrap paper at one end of the minor axis and mark where the axes cross.)
Then mark the length of half the major axis from the same corner.
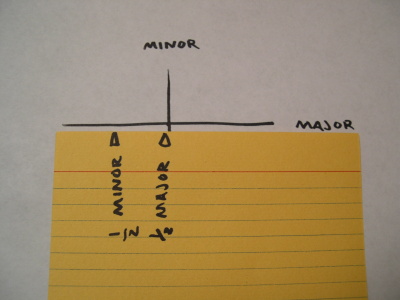
Now slide the minor mark along the major axis and the major mark along the minor axis. (The marks on the scrap paper ride the opposite rails.) Make a dot at the corner of the scrap paper at any position that satisfies these conditions.
Since the marks on the scrap paper can’t leave their rails, you’ll draw a dot right at the tip of an axis whenever the corresponding mark passes through the intersection of axes.
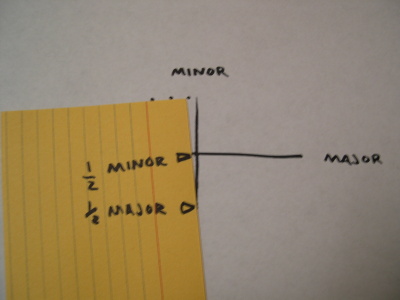
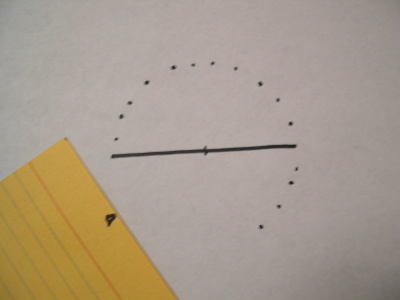
Mark dots in each quadrant of the ellipse.
See where this is leading? The major mark is still sliding along the minor axis and the minor mark is still sliding along the major axis.
Eventually, you’ll have a series of dots describing the perimeter of the ellipse you planned. The more dots you plot, the smoother the outline.
All that’s left to do is connect the dots.
A circle is a special sort of ellipse in which the major and minor axes are simply the same length. In this example, I’ve just drawn one diameter since only one mark is really needed. (Both marks would fall at the same point, technically, anchoring the card to the center of the circle.)
This technique is often attributed to Archimedes, mover of worlds. (With a long enough lever, and a place to stand…)



One Response to “The Trammel Method”
Posted by Kaitlyn on Thursday, July 8th, 2010 at 12:36 PM.
This is a great explanation! thanks!