Tag Archive: “math”
Making Ground Track Generator
I wrote a little program to make shapefiles (GIS map layers) of satellite ground tracks. Here’s the story of its development, recounted from my comments on Twitter (the internet’s water cooler).
Posted on Saturday, March 31st, 2012.
Learning Statistics by Implemetation
Over the coming summer months, I’ll be writing code to implement a variety of tests of significance. I have a modicum of statistical literacy, but I don’t have the expertise to recognize which tests are appropriate for particular problems. Rather than just learn which buttons to click in SPSS, I want to understand each common test from the inside out. Teaching a subject is a great way to learn about it, so I plan to teach the dumbest pupil of all – the unimaginative computer. I’ll post my progress here.
Posted on Thursday, May 7th, 2009.
Sigma Notation
The for loop is a useful control structure common to many programming languages. It repeats some code for each value of a variable in a given range. In C, a for loop might look like this:
for (x=1; x<=10; x=x+1)
{
/* do something ten times */
}
The initial parameter, x=1, starts a counter at one. The second parameter, x<=10, means the loop repeats until the counter reaches ten. The last parameter, x=x+1 (sometimes written x++), explains how to do the counting: add one to the counter each time through the loop.
In math, sometimes it may be necessary to add up a bunch of a related terms. For example, rather than write out 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10, the problem can be expressed with sigma notation as a sort of loop:
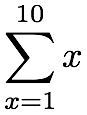
The x=1 below the big sigma starts the counter at one. The number 10 above the Σ specifies the final value of the counter. The Σ itself means to add up multiple copies of whatever follows, using integer values of x ranging from the initial 1 to the maximum 10 for each copy.
(The sum is 55.)
For simple arithmetic, this notation is hardly a simplification. However, if the terms to add are complicated, or if there are many instances of them, you’ll find this is clearly a compact and convenient way to express the sum. Plus, the Σ symbol is wicked fun to write.
The dweebs at Wikipedia have beat the programming-a-sum example to death.
Posted on Wednesday, April 16th, 2008.
Radians
I never used to understand radians. Sure, I knew how to use them in typical math problems, but splitting a circle into 2π units? Who divides a circle into six point something parts? You’ve got a useless little slice left over.
Well, remember the formula to find the circumference, C, of a circle? It’s C = πd, where d is the diameter of the circle. The diameter is simply twice the radius r, so you can also define the circumference as C = 2πr.
Consider a circle whose radius is one (the unit circle). Its circumference is simply 2π:
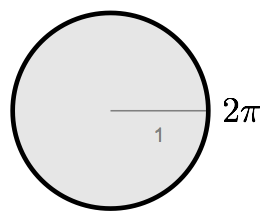
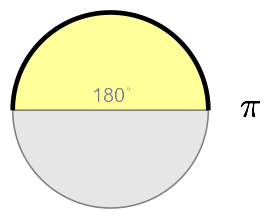
The circumference of a circle is the the distance around its edge. If you don’t go all the way around the unit circle, the length of the arc you do traverse should be less than 2π, right? It might be ¼π, ½π or plain old π if you only go an eighth, a quarter, or a half way around the circle.
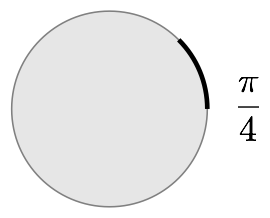
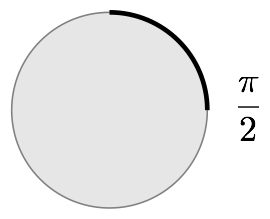
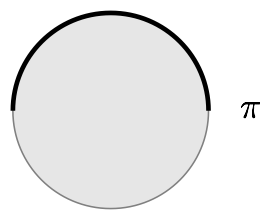
Look at the wedges created by arcs with these lengths: they describe 45, 90 and 180 degree angles. The radian equivalents of these angles are ¼π, ½π, and π.
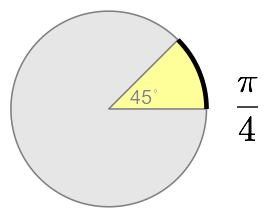
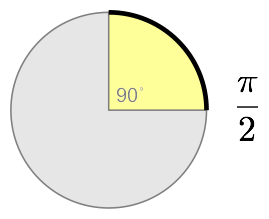
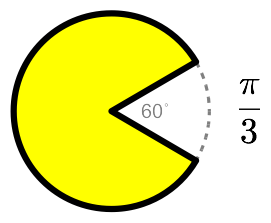
That’s it. A radian angle measurement is the length of the biggest arc that will fit in unit pacman’s mouth!
Their close connection with the basic geometry of circles makes radians convenient for a variety of purposes. But don’t worry, degrees are cool, too: 360, that’s what, almost as many days as there are in a year? Close enough for pagan ceremonies and government work!
Posted on Thursday, February 28th, 2008.
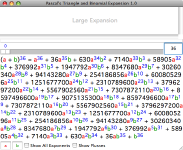
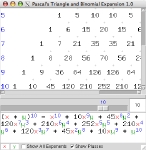
Pascal’s Triangle
Recently I was introduced (or perhaps reintroduced) to Pascal’s Triangle, an arrangement of integers that lends itself to a variety of purposes, including binomial expansion. I’ve written a little program to explore this aspect of the idea.
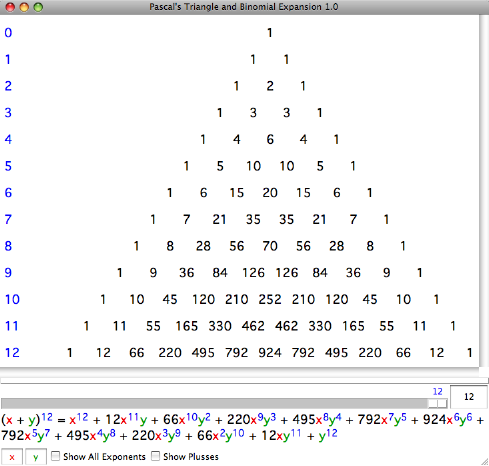
Features
- Interactively adjust the degree of the expansion to see the corresponding triangle.
- Change the binomial terms for clarity or convenience.
- Show exponents of the first and zeroth power to illustrate that the total degree of each term matches the degree of the initial expression.
- Show plus symbols in the triangle to emphasize how each row is the basis for the next.
- Mouse-over highlight of corresponding terms in triangle and expansion.
- Binomial expansions to any degree can be computed (although the triangle is only displayed for small values due to limitations of the current layout spacing).
- Click and drag in triangle to scroll or drag divider to adjust size of expansion pane.
Screenshots
Download
- Mac OS X: pt.app.zip 2.5M
- Windows: pt.exe.zip 1.3M
- Other: pt.tcl.zip 2.3K or pt.kit.zip 2.8K; requires Tcl/Tk 8.5 or a corresponding Tclkit, respectively. The Mac OS X and Windows versions are self-contained (and hundreds of times larger, unfortunately).
Posted on Monday, February 25th, 2008.
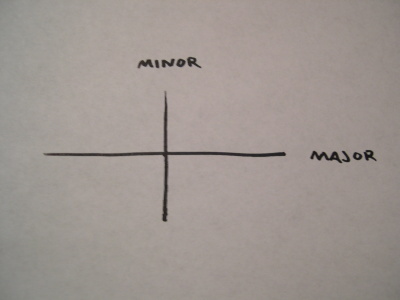
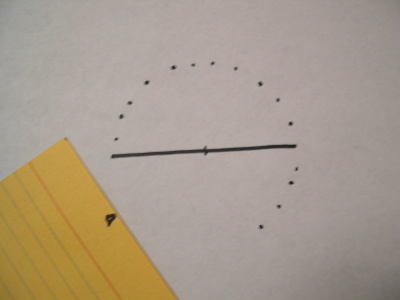
The Trammel Method
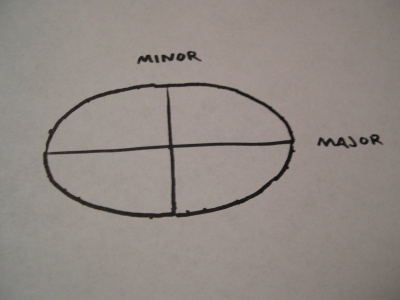
A trammel is an impediment to freedom or motion. By placing some geometric restrictions on the motion of a pen or pencil, specific types of figures can be drawn. The trammel method is one of many ways to apply this principle to the construction of ellipses (circles and ovals). It’s particularly handy if you need to draw a large curve without a compass.
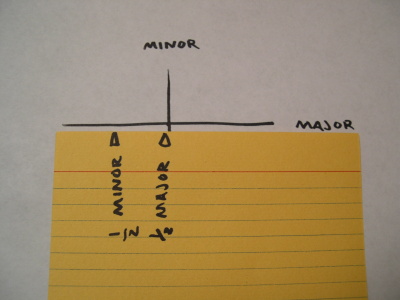
Draw a pair of perpendicular lines where you’d like to place an ellipse. I’ve labeled them as major (long) and minor (short) axes.
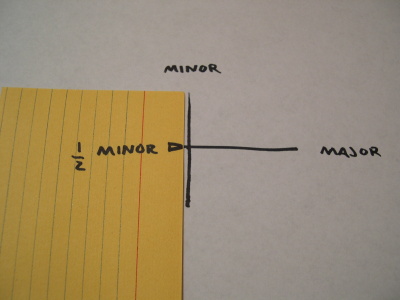
On a piece of scrap paper, mark the length of a minor radius. (Place the corner of the scrap paper at one end of the minor axis and mark where the axes cross.)
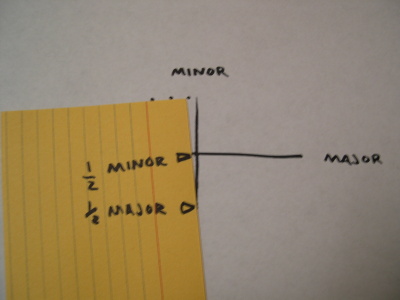
Then mark the length of half the major axis from the same corner.
Now slide the minor mark along the major axis and the major mark along the minor axis. (The marks on the scrap paper ride the opposite rails.) Make a dot at the corner of the scrap paper at any position that satisfies these conditions.
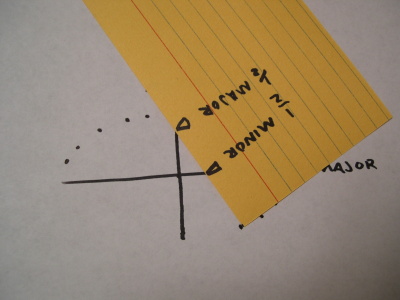
Since the marks on the scrap paper can’t leave their rails, you’ll draw a dot right at the tip of an axis whenever the corresponding mark passes through the intersection of axes.
Mark dots in each quadrant of the ellipse.
See where this is leading? The major mark is still sliding along the minor axis and the minor mark is still sliding along the major axis.
Eventually, you’ll have a series of dots describing the perimeter of the ellipse you planned. The more dots you plot, the smoother the outline.
All that’s left to do is connect the dots.
A circle is a special sort of ellipse in which the major and minor axes are simply the same length. In this example, I’ve just drawn one diameter since only one mark is really needed. (Both marks would fall at the same point, technically, anchoring the card to the center of the circle.)
This technique is often attributed to Archimedes, mover of worlds. (With a long enough lever, and a place to stand…)
Posted on Saturday, February 2nd, 2008.
Laundromat Sidewalk Math
Doing laundry is never a chore when you go to the Super-X Launderette.
You might even learn something.
Posted on Tuesday, September 25th, 2007.