Expanded Yojimbo Comment Fields
This hack tweaks Yojimbo’s bookmark, serial number, and password editors so that their comment fields expand to fill the remainder of the item pane. Before and after:
Download Expanded Yojimbo Comment Fields (33k) for Yojimbo 1.4
Download Expanded Yojimbo Comment Fields (34k) for Yojimbo 1.5.1
The download contains three modified Nib files and a readme explaining how to install them. Proceed at your own risk.
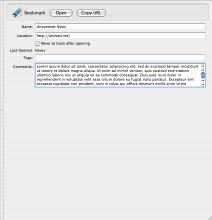
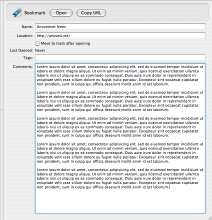
3 Responses to “Expanded Yojimbo Comment Fields”
Posted by keizo on Monday, July 23rd, 2007 at 11:29 PM.
Thanks, it’s very useful for me.
Posted by Joshua on Tuesday, January 27th, 2009 at 7:41 PM.
Thank you. This is incredibly useful, and I can’t tell you how many times I have wondered what Bare Bones was thinking by making this field so small.
Posted by Jim DeVona on Wednesday, September 2nd, 2009 at 12:32 AM.
Note: users of Yojimbo 2.0 should check out my updated version of this hack.