Radians
I never used to understand radians. Sure, I knew how to use them in typical math problems, but splitting a circle into 2π units? Who divides a circle into six point something parts? You’ve got a useless little slice left over.
Well, remember the formula to find the circumference, C, of a circle? It’s C = πd, where d is the diameter of the circle. The diameter is simply twice the radius r, so you can also define the circumference as C = 2πr.
Consider a circle whose radius is one (the unit circle). Its circumference is simply 2π:
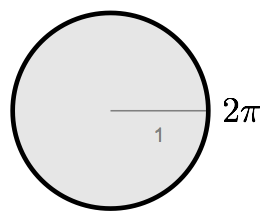
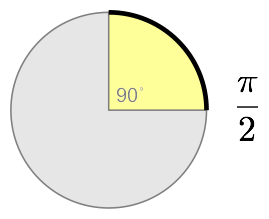
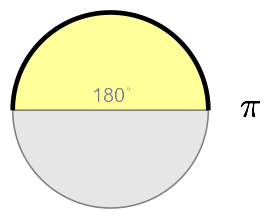
The circumference of a circle is the the distance around its edge. If you don’t go all the way around the unit circle, the length of the arc you do traverse should be less than 2π, right? It might be ¼π, ½π or plain old π if you only go an eighth, a quarter, or a half way around the circle.
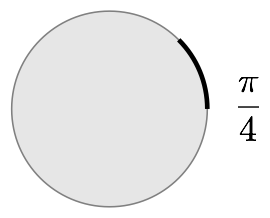
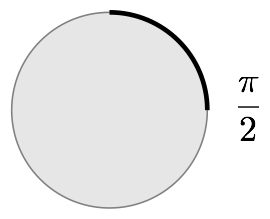
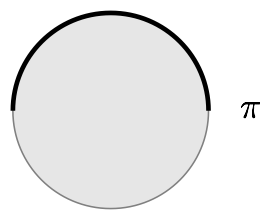
Look at the wedges created by arcs with these lengths: they describe 45, 90 and 180 degree angles. The radian equivalents of these angles are ¼π, ½π, and π.
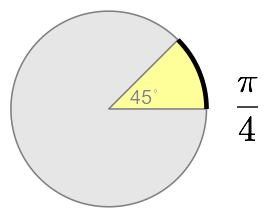
That’s it. A radian angle measurement is the length of the biggest arc that will fit in unit pacman’s mouth!
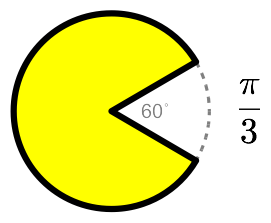
Their close connection with the basic geometry of circles makes radians convenient for a variety of purposes. But don’t worry, degrees are cool, too: 360, that’s what, almost as many days as there are in a year? Close enough for pagan ceremonies and government work!
Posted on Thursday, February 28th, 2008. Tags: math.